2023 MAA AMC 10B
- Mrs. Jones is pouring orange juice into four identical glasses for her four sons. She fills the first three glasses completely but runs out of juice when the fourth glass is only \( \frac{1}{3} \) full. What fraction of a glass must Mrs. Jones pour from each of the first three glasses into the fourth glass so that all four glasses will have the same amount of juice?
- Carlos went to a sports store to buy running shoes. Running shoes were on sale, with prices reduced by \( {20}\% \) on every pair of shoes. Carlos also knew that he had to pay a 7.5% sales tax on the discounted price. He had \ $ 43. What is the original (before discount) price of the most expensive shoes he could afford to buy?
- A \( 3 - 4 - 5 \) right triangle is inscribed in circle \( A \) , and a \( 5 - {12} - {13} \) right triangle is inscribed in circle \( B \) . What is the ratio of the area of circle \( A \) to the area of circle \( B \) ?
- Jackson's paintbrush makes a narrow strip with a width of 6.5 millimeters. Jackson has enough paint to make a strip 25 meters long. How many square centimeters of paper could Jackson cover with paint?
- Maddy and Lara see a list of numbers written on a blackboard. Maddy adds 3 to each number in the list and finds that the sum of her new numbers is 45 . Lara multiplies each number in the list by 3 and finds that the sum of her new numbers is also 45. How many numbers are written on the blackboard?
- Let \( {L}_{1} = 1,{L}_{2} = 3 \) , and \( {L}_{n + 2} = {L}_{n + 1} + {L}_{n} \) for \( n \geq 1 \) . How many terms in the sequence \( {L}_{1},{L}_{2},{L}_{3},\ldots ,{L}_{2023} \) are even?
- Square \( {ABCD} \) is rotated \( {20}^{ \circ } \) clockwise about its center to obtain square \( {EFGH} \) , as shown below. What is the degree measure of \( \angle {EAB} \) ?
- What is the units digit of \( {2022}^{2023} + {2023}^{2022} \) ?
- The numbers 16 and 25 are a pair of consecutive positive perfect squares whose difference is 9 . How many pairs of consecutive positive perfect squares have a difference of less than or equal to 2023 ?
- You are playing a game. A \( 2 \times 1 \) rectangle covers two adjacent squares (oriented either horizontally or vertically) of a \( 3 \times 3 \) grid of squares, but you are not told which two squares are covered. Your goal is to find at least one square that is covered by the rectangle. A "turn" consists of you guessing a square, after which you are told whether that square is covered by the hidden rectangle. What is the minimum number of turns you need to ensure that at least one of your guessed squares is covered by the rectangle?
- Suzanne went to the bank and withdrew \ $ 800. The teller gave her this amount using \ $ 20 bills, \ $ 50 bills, and \ $ 100 bills, with at least one of each denomination. How many different collections of bills could Suzanne have received?
- When the roots of the below polynomial are removed from the real number line, what remains is the union of 11 disjoint open intervals. On how many of these intervals is \( P\left( x\right) \) positive?
Jones 女士将橙汁倒入四个相同的玻璃杯中给她的四个儿子. 她将前三杯装满后,第四杯装到 \( \frac{1}{3} \) 满时,果汁就没有了. 要使得所有四个玻璃杯中有相同数量的橙汁, Jones 女士必须将前三个玻璃杯的每一个中橙汁的几分之几倒入第四个玻璃杯?
(A) \( \frac{1}{12} \)
(B) \( \frac{1}{4} \)
(C) \( \frac{1}{6} \)
(D) \( \frac{1}{8} \)
(E) \( \frac{2}{9} \)
Carlos 去一家体育用品店买跑鞋. 跑鞋正在促销, 每双鞋降价 20%. Carlos 还知道他必须按照折扣价的 7.5% 缴付消费税. 他有 \ $ 43. 问他能买得起的最贵的跑鞋的原价(即折扣前)是多少?
(A) \ $ 46
(B) \ $ 50
(C) \ $ 48
(D) \ $ 47
(E) \ $ 49
2023 MAA AMC 10B
三边长为 3,4,5 的直角三角形内接于圆 \( A \) ,三边长为 5,12,13 的直角三角形内接于圆 \( B \) . 问圆 \( A \) 的面积与圆 \( B \) 的面积之比是多少?
(A) \( \frac{9}{25} \)
(B) \( \frac{1}{9} \)
(C) \( \frac{1}{5} \)
(D) \( \frac{25}{169} \)
(E) \( \frac{4}{25} \)
Jackson 的画笔可以画出宽度为 6.5 毫米的窄条. Jackson 有足够的油漆来制作 25 米长的窄条. 问 Jackson 可以用颜料覆盖多少平方厘米的纸?
(A) 162,500
(B) 162.5
(C) 1,625
(D)1,625,00
(E) 16,250
2023 MAA AMC 10B
Maddy 和 Lara 看到了黑板上写着的一列数. Maddy 将这列数中的每个数加 3 ,发现她得到的所有新数的总和为 45 . Lara 将这列数中的每个数乘以 3 , 发现她得到的所有新数的总和也是 45. 问黑板上写了多少个数?
(A) 10
(B) 5
(C) 6
(D) 8
(E) 9
令 \( {L}_{1} = 1,{L}_{2} = 3 \) ,当 \( n \geq 1 \) 时, \( {L}_{n + 2} = {L}_{n + 1} + {L}_{n} \) . 问数列 \( {L}_{1},{L}_{2},{L}_{3} \) , \( \cdots ,{L}_{2023} \) 中有多少项是偶数?
(A) 673
(B) 1011
(C) 675
(D) 1010
(E) 674
2023 MAA AMC 10B
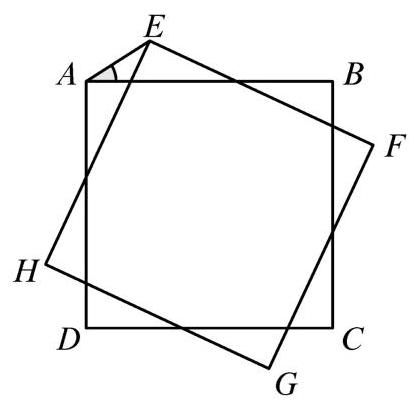
如下图所示,正方形 \( {ABCD} \) 绕其中心顺时针旋转 \( {20}^{ \circ } \) ,得到正方形 \( {EFGH} \) .
问 \( \angle {EAB} \) 的度数是多少?
(A) \( {24}^{ \circ } \)
(B) \( {35}^{ \circ } \)
(C) \( {30}^{ \circ } \)
(D) \( {32}^{ \circ } \)
(E) \( {20}^{ \circ } \)
\( {2022}^{2023} + {2023}^{2022} \) 的个位数字是多少?
(A) 7
(B) 1
(C) 9
(D) 5
(E) 3
2023 MAA AMC 10B
数 16 和 25 是一对连续的正完全平方数, 它們的差是 9 . 问有多少对连续的正完全平方数,它们的差小于或等于 2023?
(A) 674
(B) 1011
(C) 1010
(D) 2019
(E) 2017
你在玩下述的游戏. 一个 \( 2 \times 1 \) 矩形覆盖了 \( 3 \times 3 \) 方格表中的两个相邻方格 (依水平或竖直方向), 但你不知道是哪两个方格被覆盖了. 你的目标是找到至少一个被矩形覆盖的方格. 一个 “回合”是指,你猜测是某个方格,然后被告知这个方格是否被矩形覆盖. 为确保至少猜中一个被矩形覆盖的方格,你最少需要多少个回合?
(A) 3
(B) 5
(C) 4
(D) 8
(E) 6
2023 MAA AMC 10B
Suzanne 去银行提取 800 美元. 出纳员用 20 美元纸币、50 美元纸币、 100 美元纸币给了她这笔钱, 每种面值的纸币至少有一张. 问 Suzanne 得到的纸币有多少种不同的可能组合?
(A) 45
(B) 21
(C) 36
(D) 28
(E) 32
当把下面的多项式的根从实数轴上移除后, 剩下的是 11 个不相交的开区间的并集. 问在其中的多少个区间上, \( P\left( x\right) \) 为正值?
\[ P\left( x\right) = {\left( x - 1\right) }^{1}{\left( x - 2\right) }^{2}{\left( x - 3\right) }^{3}\cdots {\left( x - {10}\right) }^{10} \]
(A) 3
(B) 7
(C) 6
(D) 4
(E) 5
2023 MAA AMC 10B
- What is the area of the region in the coordinate plane defined by the below inequality?
坐标平面中由下列不等式定义的区域的面积是多少?
\[ \left| \right| x\left| {-1}\right| + \left| \right| y\left| {-1}\right| \leq 1\text{ ? } \]
(A) 2
(B) 8
(C) 4
(D) 15
(E) 12
- How many ordered pairs of integers(m, n)satisfy the equation \( {m}^{2} + {mn} + \) \( {n}^{2} = {m}^{2}{n}^{2} \) ?
- What is the least positive integer \( m \) such that \( m \cdot 2! \cdot 3! \cdot 4! \cdot 5!\cdots {16} \) ! is a perfect square?
- Define an upno to be a positive integer of 2 or more digits where the digits are strictly increasing moving left to right. Similarly, define a downno to be a positive integer of 2 or more digits where the digits are strictly decreasing moving left to right. For instance, the number 258 is an upno and 8620 is a downno. Let \( U \) equal the total number of upnos and \( D \) equal the total number of downnos. What is \( \left| {U - D}\right| \) ?
- A rectangular box \( \mathcal{P} \) has distinct edge lengths \( a, b \) , and \( c \) . The sum of the lengths of all 12 edges of \( \mathcal{P} \) is 13, the sum of the areas of all 6 faces of \( \mathcal{P} \) is \( \frac{11}{2} \) , and the volume of \( \mathcal{P} \) is \( \frac{1}{2} \) . What is the length of the longest interior diagonal connecting two vertices of \( \mathcal{P} \) ?
- Suppose that \( a, b \) , and \( c \) are positive integers such that
满足方程 \( {m}^{2} + {mn} + {n}^{2} = {m}^{2}{n}^{2} \) 的有序整数对(m, n)有多少个?
(A) 7
(B) 1
(C) 3
(D) 6
(E) 5
使得 \( m \cdot 2! \cdot 3! \cdot 4! \cdot 5!\cdots {16}! \) 是完全平方数的最小正整数 \( m \) 是多少?
(A) 30
(B) 30,030
(C) 70
(D) 1430
(E) 1001
2023 MAA AMC 10B
对于一个有 2 位或者更多位的正整数, 若它的数字从左到右严格递增, 则定义其为 “上升数”. 类似地,对于一个有 2 位或者更多位的正整数,若它的数字从左到右严格递减, 则定义其为 “下降数”. 例如, 数 258 是上升数, 8620 则是下降数. 令 \( U \) 为上升数的总个数, \( D \) 为下降数的总个数. 问 \( \left| {U - D}\right| \) 是多少?
(A) 512
(B) 10
(C) 0
(D) 9
(E) 511
一个长方体盒子 \( \mathcal{P} \) 的三条不同的棱长为 \( a, b, c.\mathcal{P} \) 的所有 12 条棱的长度之和为 \( {13},\mathcal{P} \) 的所有 6 个面的面积之和为 \( \frac{11}{2} \) ,并且 \( \mathcal{P} \) 的体积为 \( \frac{1}{2} \) . 问连接 \( \mathcal{P} \) 的两个顶点, 且在其内部的对角线最长是多少?
(A) 2
(B) \( \frac{3}{8} \)
(C) \( \frac{9}{8} \)
(D) \( \frac{9}{4} \)
(E) \( \frac{3}{2} \)
2023 MAA AMC 10B
\[ \frac{a}{14} + \frac{b}{15} = \frac{c}{210}. \]
Which of the following statements are necessarily true?
I. If \( \gcd \left( {a,{14}}\right) = 1 \) or \( \gcd \left( {b,{15}}\right) = 1 \) or both, then \( \gcd \left( {c,{210}}\right) = 1 \) .
II. If \( \gcd \left( {c,{210}}\right) = 1 \) , then \( \gcd \left( {a,{14}}\right) = 1 \) or \( \gcd \left( {b,{15}}\right) = 1 \) or both.
III. \( \gcd \left( {c,{210}}\right) = 1 \) if and only if \( \gcd \left( {a,{14}}\right) = 1 \) and \( \gcd \left( {b,{15}}\right) = 1 \) .
假设 \( a, b, c \) 是正整数,满足
\[ \frac{a}{14} + \frac{b}{15} = \frac{c}{210} \]
问以下哪些陈述一定是正确的?
I. 如果 \( \gcd \left( {a,{14}}\right) = 1 \) ,或者 \( \gcd \left( {b,{15}}\right) = 1 \) ,或者两式都成立,那么 \( \gcd \left( {c,{210}}\right) = 1 \) .
II. 如果 \( \gcd \left( {c,{210}}\right) = 1 \) ,那么 \( \gcd \left( {a,{14}}\right) = 1 \) ,或者 \( \gcd \left( {b,{15}}\right) = 1 \) ,或者两式都成立.
III. \( \gcd \left( {c,{210}}\right) = 1 \) ,当且仅当 \( \gcd \left( {a,{14}}\right) = 1 \) ,并且 \( \gcd \left( {b,{15}}\right) = 1 \) . 这里 gcd 表示最大公约数.
(A) I, II, and III | I, II 和 III
(B) I only | 只有 I
(C) I and II only | 只有 I 和 II
(D) III only | 只有 III
(E) II and III only | 只有 II 和 III
2023 MAA AMC 10B
- Sonya the frog chooses a point uniformly at random lying within the square \( \left\lbrack {0,6}\right\rbrack \times \left\lbrack {0,6}\right\rbrack \) in the coordinate plane and hops to that point. She then chooses a distance uniformly at random in the interval \( \left\lbrack {0,1}\right\rbrack \) and a direction uniformly at random from \{north, east, south, west\}. All her choices are independent. She now hops the chosen distance in the chosen direction. What is the probability that she lands outside the square?
- Four congruent semicircles are drawn on the surface of a sphere with radius 2 , as shown, creating a closed curve that divides its surface into two congruent regions. The length of the curve is \( \pi \sqrt{n} \) . What is \( n \) ?
- Each of 2023 balls is randomly placed into one of 3 bins. Which of the following is closest to the probability that each of the bins will contain an odd number of balls?
- How many distinct values of \( x \) satisfy \( \lfloor x{\rfloor }^{2} - {3x} + 2 = 0 \) , where \( \lfloor x\rfloor \) denotes the greatest integer less than or equal to \( x \) ?
- An arithmetic sequence of positive integers has \( n \geq 3 \) terms, initial term \( a \) , and common difference \( d > 1 \) . Carl wrote down all the terms in this sequence correctly except for one term, which was off by 1 . The sum of the terms he wrote down was 222 . What is \( a + d + n \) ?
- What is the length of the boundary of the region in the \( {xy} \) plane consisting of points of the form \( \left( {{2u} - {3w}, v + {4w}}\right) \) where \( 0 \leq u \leq 1,0 \leq v \leq 1 \) , and \( 0 \leq w \leq 1 \) ?
- A regular pentagon with area \( 1 + \sqrt{5} \) is printed on paper and cut out. All five vertices are folded to the center of the pentagon, creating a smaller pentagon. What is the area of the new pentagon?
青蛙 Sonya 在坐标平面中由 \( \left\lbrack {0,6}\right\rbrack \times \left\lbrack {0,6}\right\rbrack \) 形成的正方形内均匀随机的选择一个点,并且跳到该点. 然后,她在区间 \( \left\lbrack {0,1}\right\rbrack \) 中均匀随机的选择一个距离,并从 \( \{ \) 东、南、西、北 \( \} \) 中均匀随机的选择一个方向. 她的所有选择都是独立的. 现在,她朝着选定的方向跳跃选定的距离. 问她落在正方形外的概率是多少?
(A) \( \frac{1}{6} \)
(B) \( \frac{1}{12} \)
(C) \( \frac{1}{4} \)
(D) \( \frac{1}{10} \)
(E) \( \frac{1}{9} \)
2023 MAA AMC 10B
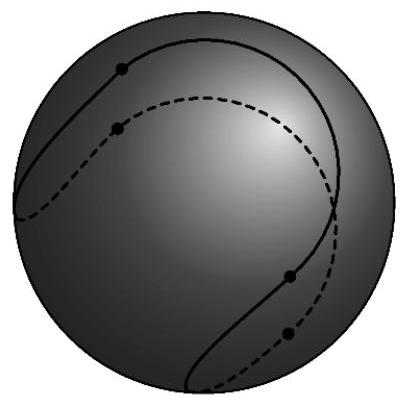
如图所示,在半径为 2 的球体表面绘制了四个全等的半圆,形成了一条将球表面分为两个全等区域的闭合曲线. 曲线的长度为 \( \pi \sqrt{n} \) . 问 \( n \) 是多少?
(A) 32
(B) 12
(C) 48
(D) 36
(E) 27
将 2023 个球中的每个球都随机放入 3 个箱子中的一个. 问以下哪一项最接近每个箱子中都有奇数个球的概率?
(A) \( \frac{2}{3} \)
(B) \( \frac{3}{10} \)
(C) \( \frac{1}{2} \)
(D) \( \frac{1}{3} \)
(E) \( \frac{1}{4} \)
2023 MAA AMC 10B
满足 \( \lfloor x{\rfloor }^{2} - {3x} + 2 = 0 \) 的不同的 \( x \) 值有多少个? 这里 \( \lfloor x\rfloor \) 表示小于或等于 \( x \) 的最大整数.
(A) an infinite number | 无穷多个
(B) 4
(C) 2
(D) 3
(E) 0
一个由正整数组成的等差数列的项数是 \( n \geq 3 \) ,首项是 \( a \) ,公差是 \( d > 1 \) . Carl 写出了这个数列中的所有项, 除一项与正确值相差 1 外, 写出的其他项都是正确的. 他写下的所有项的总和是 222. 问 \( a + d + n \) 是多少?
(A) 24
(B) 20
(C) 22
(D) 28
(E) 26
2023 MAA AMC 10B
在 \( {xy} \) 平面中,考虑形如 \( \left( {{2u} - {3w}, v + {4w}}\right) \) 的点,其中 \( 0 \leq u \leq 1,0 \leq v \leq 1 \) , \( 0 \leq w \leq 1 \) . 问这些点组成的区域的边界的长度是多少?
(A) \( {10}\sqrt{3} \)
(B) 13
(C) 12
(D) 18
(E) 16
在纸上打印并剪下一个面积为 \( 1 + \sqrt{5} \) 的正五边形. 将所有的五个顶点都折叠到五边形的中心,形成一个较小的五边形. 问新五边形的面积是多少?
(A) \( 4 - \sqrt{5} \)
(B) \( \sqrt{5} - 1 \)
(C) \( 8 - 3\sqrt{5} \)
(D) \( \frac{\sqrt{5} + 1}{2} \)
(E) \( \frac{2 + \sqrt{5}}{3} \)
2023 MAA AMC 10B
Answers.
CBDCA EBABC BCBCC EDEBA EBBEB